Arithmetic Topics for Online Tests

Ratio & Proportion

Ratios: A ratio is a way to compare two or more quantities. It is often expressed in the form of a:b, where a and b are the quantities being compared. Ratios can be simplified by dividing both terms by their greatest common divisor.

ProportionsA proportion is an equation that states that two ratios are equal. For example, if a/b = c/d ,then a,b,c, and d are said to be in proportion. To solve proportions, you can use cross-multiplication.

Formulas and Key Points:

1. Simplifying Ratios: Divide both terms of the ratio by their greatest common divisor.
• Example: To simplify the ratio 12:16, divide both terms by 4 to get 3:4.
2. Proportion Formula:
• If a/b = c/d, then a*d = b*c
• This can be used to find the missing term in a proportion.
3. Finding Ratios:
• To find the ratio between two quantities, divide each quantity by a common term and simplify.

Simple Interest

Introduction: Simple Interest (SI) is a method of calculating the interest charged on a sum of money (the principal) over a certain period at a fixed rate. Unlike compound interest, simple interest does not take into account the interest that accumulates on the interest already earned. Instead, it is calculated only on the principal amount throughout the period.

Key Terms

1. Principal (P): The original sum of money lent or invested.
2. Rate of Interest (R): The percentage at which the interest is charged or earned.
3. Time (T): The duration for which the money is borrowed or invested, usually expressed in years.
4. Simple Interest (SI): The amount earned or paid for the use of money over time.

Formula: SI = (P x R x T) / 100

Additional Formulas:
Calculating Total Amount (A): The total amount payable or receivable at the end of the time period, including both principal and interest.
A = P+SI

Substituting the value of SI, we get:
A=P+ (PxRxT)/100

Finding Principal (P): When the simple interest, rate, and time are known.
P= (SIx100)/(RxT)

Finding Rate (R): When the simple interest, principal, and time are known.
R= (SIx100)/(PxT)

Finding Time (T): When the simple interest, principal, and rate are known.
T= (SIx100)/(PxR)

Examples of Simple Interest
Example 1: If you invest $1,000 (P) at an annual interest rate of 5% (R) for 3 years (T),
the simple interest (SI) will be: SI= (1000x5x3)/100 = 150
So, the simple interest is $150.

Example 2: You borrowed $2,000 at a rate of 6% per annum for 4 years. The interest payable will be:
SI= (2000x6x4)/100 = 480
The interest payable is $480.

Profit & Loss

Profit: Profit is the financial gain obtained when the selling price (SP) of an item is greater than its cost price (CP). The formula for calculating profit is:

• Profit = Selling Price (SP) - Cost Price (CP)

Loss: Loss occurs when the cost price (CP) of an item is greater than its selling price (SP). The formula for calculating loss is:

• Loss = Cost Price (CP) - Selling Price (SP)

Formulas and Key Points:

1. Profit Percentage:
   Profit Percentage = (Profit / Cost Price) * 100
2. Loss Percentage:
   Loss Percentage = (Loss / Cost Price) * 100
3. Relation Between Selling Price and Cost Price:
   SP = CP * (1 + (Profit %)/100) [If profit]
   SP = CP * (1 - (Loss %)/100) [If loss]

Averages

Average: The average of a set of numbers is the value that represents the central or typical point of the data set. It is commonly referred to as the arithmetic mean.

Formulas for Averages:

1. Arithmetic Mean (Average):
   Average = (Sum of all values) / (Number of values)
2. Weighted Average:
   Weighted Average = (Σ(Value x Weight)) / (Σ Weights)

Key Points:

• Arithmetic Mean: This is the most commonly used measure of average. It is calculated by dividing the sum of all values by the number of values.
• Weighted Average: This type of average takes into account different weights assigned to values. It is useful when certain values contribute more to the overall mean than others.

Percentages

Introduction: Percentages represent a fraction of 100. They are used to express how a number compares to a whole, which is often referred to as 100%. The percentage value can be used in various financial calculations, comparisons, and statistics.

Basic Formula:

• Percentage = (Part / Whole) * 100

Key Formulas:

1. Finding Percentage:
   To find what percentage a number is of another number, use the formula:
   Percentage = (Part / Whole) * 100
2. Percentage Increase:
   To calculate the percentage increase from an old value to a new value:
   Percentage Increase = [(New Value - Old Value) / Old Value] * 100
3. Percentage Decrease:
   To calculate the percentage decrease from an old value to a new value:
   Percentage Decrease = [(Old Value - New Value) / Old Value] * 100
4. Finding the Whole from a Percentage:
   To determine the original amount when you know the percentage and the part:
   Whole = (Part / Percentage) * 100

Speed, Distance, and Time

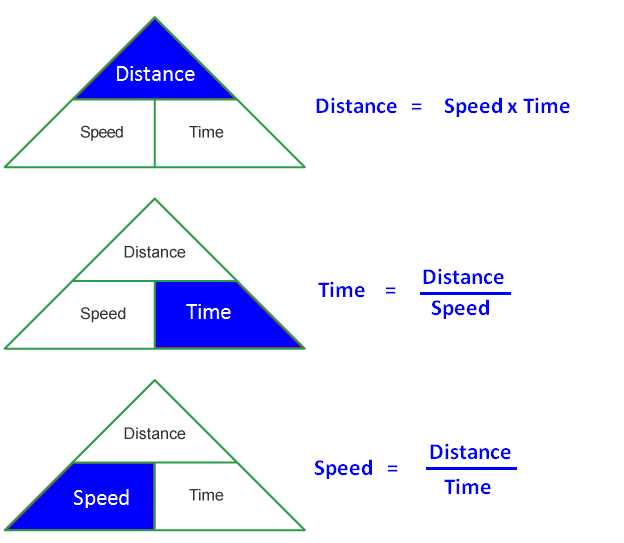
Introduction: Speed, distance, and time are fundamental concepts in motion and transportation. They are related by simple mathematical formulas that help calculate any one of these values when the other two are known.

Basic Formulas:

• Speed = Distance / Time
• Distance = Speed * Time
• Time = Distance / Speed

Key Formulas and Calculations:

1. Average Speed:
   When you travel different distances at different speeds, the average speed is calculated as:
   Average Speed = Total Distance / Total Time
2. Speed Conversion:
   To convert speed between units (e.g., km/h to m/s):
   Speed in m/s = Speed in km/h * (1000 / 3600)
   Speed in km/h = Speed in m/s * (3600 / 1000)
3. Time Conversion:
   To convert time between units (e.g., hours to minutes):
   Time in minutes = Time in hours * 60
   Time in hours = Time in minutes / 60

Ages

Introduction: Problems involving ages often require setting up equations based on the relationship between the ages of different individuals. These problems typically involve simple algebraic operations.

Basic Formulas:

• Current Age = Age in Past + Number of Years Passed
• Age in Future = Current Age + Number of Years in Future
• Difference in Ages = Absolute Difference Between Two Ages

Key Formulas and Calculations:

1. Age Difference:
   The difference in ages remains constant over time. If person A is 10 years older than person B, this difference will always be 10 years.
2. Combined Age:
   The sum of the ages of two or more people at any point in time can be calculated by adding their individual ages.
3. Finding Past Ages:
   To find a person's age at a past time, subtract the number of years that have passed from their current age.

Algebra

Introduction: Algebra involves using symbols, typically letters, to represent numbers and express mathematical relationships. It includes solving equations, simplifying expressions, and working with functions.

Basic Concepts:

• Variables: Symbols (often letters) used to represent unknown values.
• Expressions: Combinations of variables, numbers, and operations (e.g., 2x + 3).
• Equations: Mathematical statements that assert the equality of two expressions (e.g., 2x + 3 = 7).
• Inequalities: Statements that describe the relative size or order of two values (e.g., x > 5).

Key Formulas and Techniques:

1. Solve Linear Equations:
   To find the value of the variable that makes the equation true (e.g., x + 5 = 12).
2. Factor Quadratic Expressions:
   Expressing a quadratic equation in its factored form (e.g., x^2 + 5x + 6 = (x + 2)(x + 3)).
3. Use the Quadratic Formula:
   Solving quadratic equations of the form ax^2 + bx + c = 0 using x = (-b ± √(b² - 4ac)) / 2a.

Pipes and Cisterns

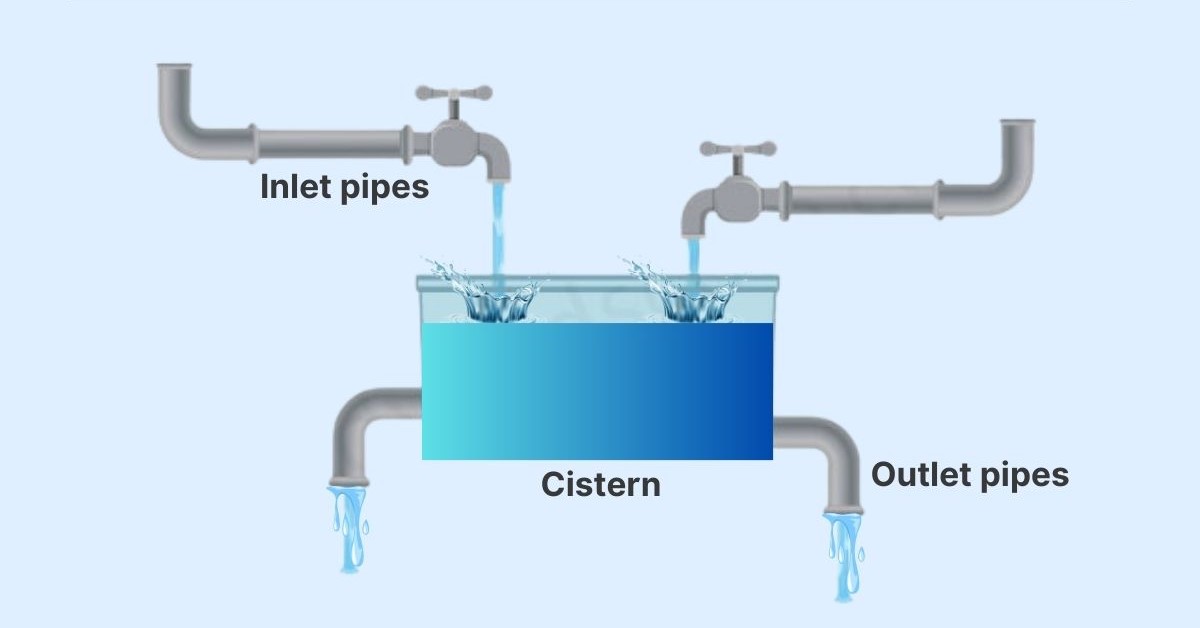
Introduction: Pipes and cisterns problems involve calculating the time required to fill or empty a tank given different rates of flow. These problems often require the use of work rates and understanding of the combined or individual rates of the pipes.

Basic Concepts:

• Work Rate: The rate at which a pipe fills or empties a tank, typically measured in units of volume per time (e.g., liters per hour).
• Time: The duration required to fill or empty a tank, calculated based on the work rates of the pipes.
• Combined Rate: The total rate at which multiple pipes fill or empty a tank when working together.

Key Formulas:

1. Time = Volume / Rate:
   To find the time required to fill or empty a tank, divide the total volume by the rate of flow.
2. Combined Rate:
   When pipes work together to fill or empty a tank, the combined rate is the sum of their individual rates if they are filling or the difference if they are emptying.
3. Time Taken by Each Pipe:
   If Pipe A fills the tank in 'a' hours and Pipe B fills it in 'b' hours, then the time taken to fill the tank together is given by: Time = 1 / (1/a + 1/b).